Rearranging Nucleons – ⟨ me

Once praised as the carbon-free energy source of the future, now mainly discredited for producing radioactive waste and having rendered entire regions uninhabitable, nuclear power plants have been a topic for discussion for a long time. This post tries to approach the topic soberly, explaining the physical basics of nuclear power.

From Electron Arrangements…

Put simply, we obtain most of the energy we need in our everyday lives by optimizing the arrangements of electrons in atoms $\left [1 \right ]$ . This is how a fire works: given enough heat, the atoms in oxygen and the fuel form new covalent bonds, optimizing their electron arrangements.

Such processes typically release heat on the order of $1 \text{ eV}$ per reaction ( $1 \text{ eV}$ roughly corresponds to $10^{-25}$ of the energy in a chocolate bar $\left [2 \right ]$ ). This may sound like little, but since usually a vast number of molecules react every second, the total heat output can be considerable. A fire for example can easily throw enough $1 \text{ eV}$ energy quanta at you to get you killed.

… to Nucleon Arrangements

But what if we still tried to optimize this? If instead of fidling around with electrons we would start trying to optimize the arrangements of protons and neutrons – collectively called nucleons – in atoms? A fascinating question, yet dangerous at the same time.

Processes in which the arrangement of nucleons are changed are better known as nuclear reactions. Following this logic, it would actually make sense to call normal chemical reactions “shell reactions”, but nobody does that.

**Figure 1:** The well-known depiction of the atom. While normal chemical reactions only involve electrons, so-called nuclear reactions involve protons and neutrons. (Source: bar.wikipedia.org)

What makes neutrons and protons fundamentally different from electrons is that they are able to interact via the nuclear force. The nuclear force is a residual effect of the so-called strong force which is – unnecessary pause to build up tension – very strong. As a result, nucleon-nucleon bonds are much stronger than nucleon-electron bonds. While electrons have binding energies on the order of $1 \text{ eV}$ (as discussed before), the binding energies of nucleons are on the order of $1`000`000 \text{ eV} = 1 \text{ MeV}$ (see diagram below).

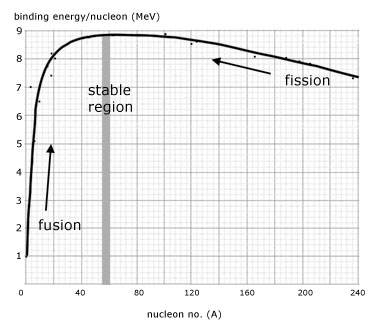
**Figure 2:** The binding energy per nucleon (protons and neutrons) in atoms. The x-axis states the total number of nucleons in the atom.
(Source: a-levelphysicstutor.com)

So, a reaction optimizing the arrangements of nucleons in atoms and releasing a part of their binding energy would be a million times more powerful than a combustion reaction. But how would such a reaction look like?

The answer lies in the diagram above. The average binding energy per nucleon depends on the total number of nucleons $A$ present in the atom. The curve shown on above diagram peaks at $A = 56$ and drops both for smaller and larger $A$ s. Now, let’s consider a large atom, for example one with $A = 240$ . Its total binding energy is roughly $240 \cdot 7.5 \text{ MeV} = 1`800 \text{ MeV}$ . If this atom could somehow divide itself into two smaller atoms, for example with $A = 120$ each, it could enhance its total binding energy: now each of the nucleons in the two daughter atoms would feel a binding energy of roughly $8.5 \text{ MeV}$ , giving $240 \cdot 8.5 \text{ MeV} = 2`040 \text{ MeV}$ in total. The fission of the large atoms would therefore yield $240 \text{ MeV}$ released in the form of heat.

Uranium Fission

These principles apply directly to the nuclear fission of Uranium employed in nuclear power plants. When a Uranium atom ( $_{92}^{235}\text{U}_{143}$ ) captures a free-flying neutron ( $n$ ), it enters an excited state with internal vibrations ( $_{92}^{236}\text{U}^{\ast}_{144}$ ):

$_{92}^{235}\text{U}_{143} + n \rightarrow \ _{92}^{236}\text{U}^{\ast}_{144}$

**Figure 3:** The Uranium atom captures a free-flying neutron and enters an unstable excited state.

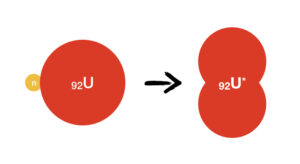
In above formula, the notation $_{\text{P}}^{\text{A}}\text{E}_{\text{N}}$ was used, where $\text{E}$ is the abbreviation of the atom (Uranium), $\text{P}$ is the number of protons in the atom, $\text{N}$ the number of neutrons and $\text{A}$ the total number of nucleons ( $\text{A} = \text{P} + \text{N}$ ). The excitation is marked by the asterisk.

The vibrations in the excited state can be strong enough to cause the Uranium atom to divide into two smaller atoms:

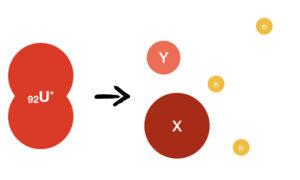
$_{92}^{236}\text{U}^{\ast}_{144} \rightarrow X + Y + \overline{2.43 n} + Q$

**Figure 4:** An excited Uranium atom decays into two daughter atoms X and Y, as well as three neutrons.

$X$ and $Y$ are the two daughter atoms. They are not always the same. It could be $_{36}^{92}\text{Kr}_{56}$ and $_{56}^{141}\text{Ba}_{85}$ $\left [3 \right ]$ , but many other combinations are possible too. $\overline{2.43 n}$ means that on average, 2.43 neutrons are released per decay. Of course the actual number is always a positive integer.

Finally, $Q$ is the heat that is released in the decay. It is this heat that nuclear power plants use. On average, it amounts to $204 \text{ MeV}$ per Uranium fission, of which $192 \text{ MeV}$ are useable (some of the energy is carried away by neutrinos).

Where does this energy come from? I’m sure you guessed it: the optimization of nucleon arrangements. Since the daughter atoms $X$ and $Y$ have smaller $A$ s, their binding energies per nucleon are larger than the one of $_{92}^{236}\text{U}_{144}$ (see Figure 2). It is exactly this difference in binding energy that is released in the form of heat.

Hazards

It is not surprising that a reaction 200 million times more powerful than a combustion comes with hazards. These have to be well contained to avoid serious harm.

The first hazard is that of a chain reaction. As discussed above, a free-flying neutron is required to start the fission reaction of $_{92}^{235}\text{U}_{143}$ . In order to guarantee continuous operation in a power plant, the right amount of free neutrons therefore needs to be available inside the reactor at all times. The emphasis is on right amount here. Of the 2.43 neutrons that are released in a reaction on average, only one should stick around to induce another fission. If it’s more, the number of fissions increases – necessary pause to build up tension – exponentially! For example, let’s assume that two of the released neutrons are able to induce new reactions. Then one fission induces two fissions, which induce four fissions, which induce eight fissions, which induce… you get the point. After a very short time so many fissions take place at the same time that an insane amount of energy is released – the reactor blows up. Nobody in their right mind could want such a chain reaction. On the other hand, if less than one neutron sticks around, the reactor shuts down. After one generation, only half as many fissions are induced, then a quarter, then an eighth, and so on. Therefore, continuously operating a nuclear reactor critically depends on having one – and exactly one – neutron per fission that is able to induce another fission. In order to ensure this in practice, a fascinating solution is employed in power plants, which I will discuss in another post soon to follow.

The second hazard is nuclear radiation. The problem with optimizing nucleon arrangements in atoms is that the optimization doesn’t simply stop. The daughter atoms continue to optimize their nucleon arrangements in spontaneous decays. The most famous one is probably the alpha decay, where two protons and two neutrons are released. But there are others, such as the beta decay, where the decaying atom releases a free electron or the gamma decay, where a photon is emitted. An overview over the different spontaneous decays is given in Figure 5.

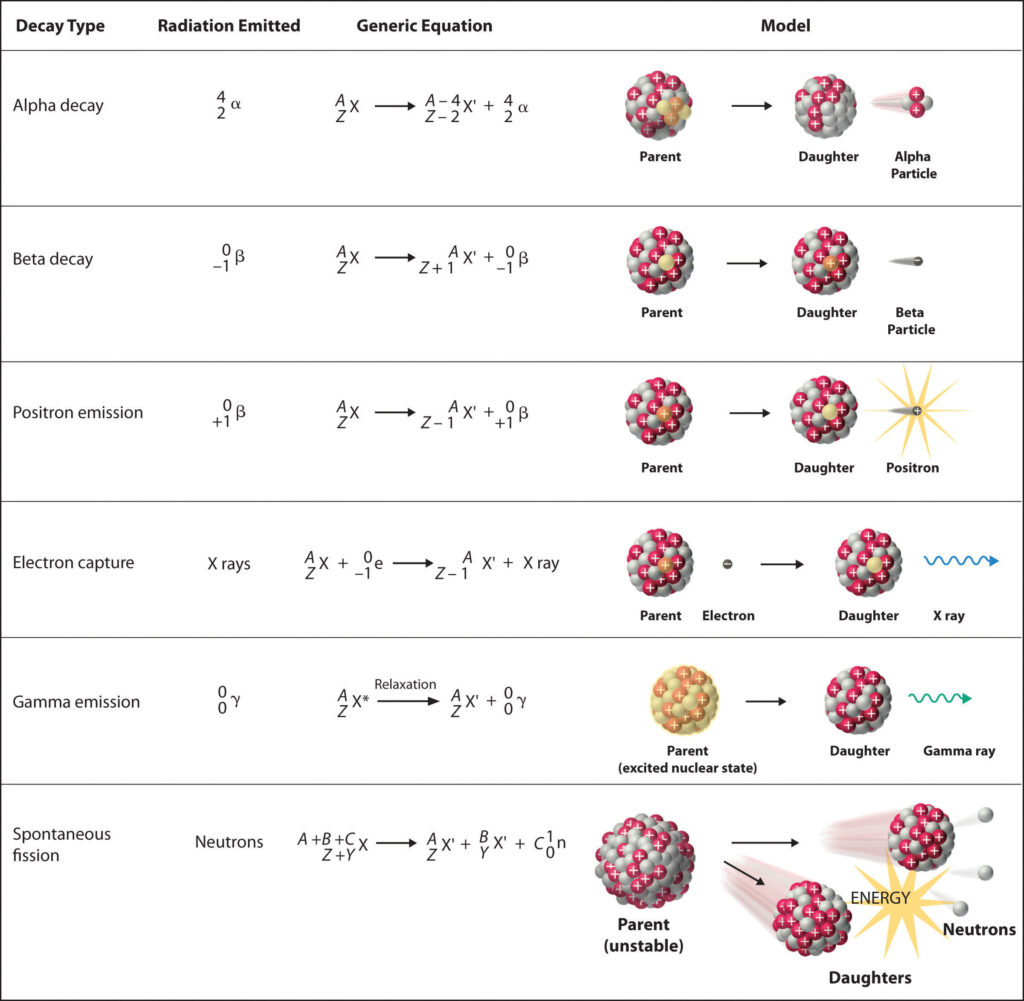
**Figure 5:** Overview over all spontaneous nuclear decays. The emitted particles are known as radioactive radiation.
(Source: chem.libretexts.org)

These spontaneous decays happen naturally around us all the time, but since earth has been around for a while now, the number of decays taking place in a given time interval is usually quite small. Unstable atoms have had ample time to decay into more stable forms. But by combining $_{92}^{236}\text{U}_{144}$ with an additional neutron, thus causing it to divide artificially, daughter atoms are created that need not be stable. They continue to decay spontaneously and to release radiation – for centuries to come.

This radiation is harmful for humans. Not because of its composition, but because of its energy. Let’s consider gamma radiation for example. “Gamma radiation” is a fancy word for light with a lot of energy, it consists of nothing other than energetic photons. But while photons with energies in the $\text{eV}$ range (for example emitted by a fire) stimulate our retinas and enable us to see $\left [4 \right ]$ , photons in the $\text{MeV}$ range (“gamma particles”) can directly kill our cells or knock out parts of our DNA, possibly leading to cancer and gene mutations.

Politics

I feel like I can’t end this post without having given my opinion on whether we should use nuclear power plants. My short answer is: in the current form, no. Even if we could ensure safe operation of the reactors, it is simply irresponsible to produce nuclear waste that will emit deadly radiation for centuries to come.

However, I agree with Switzerland’s policy $\left [6 \right ]$ to use the existing nuclear power plants until their target expiration date, if the remaining time is used to build up the reusable energy infrastructure to replace them.

In addition, I believe that we should still invest resources into nuclear power plant research. Given the global energy crisis that we’re facing, it seems a good idea to try out all possible solutions. Furthermore, we desperately need good solutions to deal with the nuclear waste that already exists and to dismantle the existing power plants. Ceasing to research into nuclear power plants because “nuclear” sounds bad certainly is a terrible idea.

We have to make sure that we, as a society, are in the role of the sorcerer – having knowledge of the things we set in motion –, instead of the apprentice:

Deep and deeper grows the water
On the stairs and in the hall,
Rushing in with roar and clatter –
Lord and master, hear me call!
Ah, here comes the master –
Sore, sir, is my strait;
I raised this spirit faster
Far than I can lay’t.
“Broom, avaunt thee!
To thy nook there!
Lie, thou spook, there!
Only answer,
When for mine own ends I want thee,
I, the master necromancer!”
from The Sorcerer’s Apprentice by Johann W. v. Goethe (translation by W.E. Aytoun and T. Martin)

Sources

Many of the facts presented in this post were taken from the lecture notes of the lecture “Einführung in die Kern- und Teilchenphysik”, ETH Zürich. Unfortunately, I am not allowed to share them. But videos of the lectures are available here: video.ethz.ch.

$\left [1 \right ]$ bfe.admin.ch
$\left [2 \right ]$ wolframalpha.com
$\left [3 \right ]$ en.wikipedia.org
$\left [4 \right ]$ courses.lumenlearning.com
$\left [5 \right ]$ livescience.com
$\left [6 \right ]$ bfe.admin.ch

Source featured image: energisch.ch