Anti-Gravitation

Newtons Gravitationstheorie

Der Apfel fällt vom Baum wegen der anziehenden Gravitationskraft der Erde. Gähn. Auch Newtons Gravitationsformel

ist mittlerweile mehrere Jahrhunderte alt und wird wohl von vielen als alter Hut abgetan. Fälschlicherweise. Denn tatsächlich gibt es im Zusammenhang mit dieser Formel Fragen, welche die moderne Physik bis heute beschäftigen.

Die erste dreht sich um die Massen . Was genau ist mit ihnen gemeint? Es gibt nämlich im Grunde zwei verschiedene Massen: diejenige, auf die die Gravitationskraft wirkt und diejenige, die sich in Form von Trägheit Beschleunigungen widersetzt. Erstere wird die schwere Masse genannt, zweitere die träge Masse. Mit  sind hier die schweren Massen der Objekte gemeint. Im Grunde könnten diese verschieden von den trägen Massen sein, denn der Zusammenhang zwischen wie stark ein Objekt Gravitation ausübt und wie stark es sich Geschwindigkeitsänderungen widersetzt scheint nicht offensichtlich.

Die Gleichheit

wurde schliesslich von niemand geringerem als Albert Einstein als Axiom, dem sogenannten Äquivalenzprinzip, für seine Allgemeine Relativitätstheorie angenommen. Das Äquivalenzprinzip kann in Gedankenexperimenten plausibilisiert werden und ist experimentell bis zu einer hohen Präzision nachgewiesen worden: bis jetzt auf (siehe erste Resultate der MicroSCOPE Mission [1]), bis Ende 2019 dürfte eine Präzision von  erreicht worden sein. Für Materie ist die Gleichheit also experimentell ziemlich gut gesichert.

Gravitation der Antimaterie

Für Antimaterie sieht dies jedoch anders aus. Während die meisten Physikerinnen und Physiker annehmen, dass das Äquivalenzprinzip auch für Antimaterie gilt, ist die experimentelle Beweisgrundlage dafür dürftig. Die bisher einzige direkte Messung mit Anti-Wasserstoff konnte das Verhältnis der beiden Massen (der Strich über dem gibt an, dass es sich um Antiteilchen handelt) nur auf

einschränken [2]. Die obere Grenze 110 bedeutet konkret, dass die Gravitationskraft, die ein Anti-Wasserstoffatom spürt, 110 mal grösser sein könnte als diejenige, die auf ein normales Wasserstoffatom wirkt. Sie könnte aber auch nur 50 mal grösser sein, oder 10 mal grösser, vielleicht aber auch 0.5 mal kleiner, oder Anti-Wasserstoffatome könnten auch gar keine Gravitationskraft spüren – wir wissen es einfach nicht. Richtig interessant wird es, wenn man die negativen Zahlen betrachtet (die untere Grenze ist ja eine negative Zahl). Dies wirft nämlich eine weitere Frage bezüglich Newtons Formel auf: was passiert, wenn die Massen negativ werden? Für die trägen Massen würde das überhaupt keinen Sinn ergeben (was ist schon negative Trägheit?), aber für die schweren Massen schon: ist eine der beiden Massen in Newtons Formel negativ, so stossen sich die beiden einfach gegenseitig ab. Sind beide negativ, so ziehen sie sich wiederum an. Ein negatives Massenverhältnis würde bedeuten, dass Antiteilchen negative schwere Massen hätten und deshalb von normaler Materie abgestossen werden würden. Gäbe es einen “Anti-Apfel”, so würde dieser dann im Gravitationsfeld der Erde nach oben fliegen, von der Erde weg. Das mag zugegebenermassen ziemlich absurd klingen. Tatsächlich gibt  es aber etliche Physikerinnen und Physiker, die sich mit negativen schweren Massen beschäftigt haben und daraus elegante Lösungen zu grossen Problemen der modernen Physik ableiten konnten.

Gravitations-Dipole

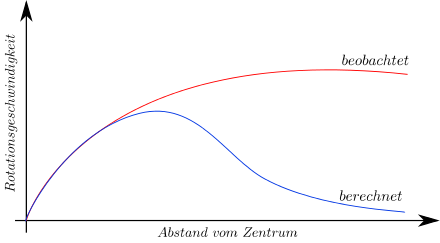
Während einer Führung am CERN (mehr dazu unter Semesterarbeit am CERN) wurde ich auf ein Forschungspaper von Hajdukovic [3] aufmerksam gemacht. Dieses liefert eine alternative Erklärung zu den anomalen Galaxie-Rotationskurven, aufgrund deren die Existenz von Dunkler Materie postuliert wurde (mehr dazu auf Wikipedia [4]).

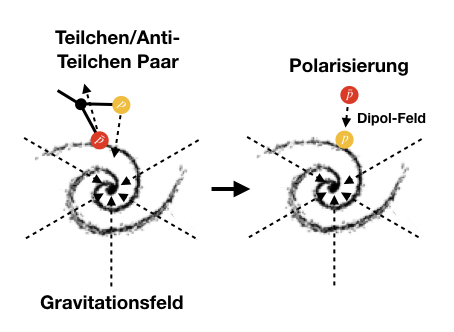
Hajdukovic basiert seine Theorie auf einem Massenverhältnis , sprich , und kann damit die anomalen Rotationskurven mit der Existenz von Gravitations-Dipolen erklären. Im Vakuum des Weltalls treten immer wieder Quantenfluktuationen auf: spontan werden Paare bestehend aus einem Teilchen und dem entsprechenden Antiteilchen gebildet, die nach kurzer Zeit wieder verschwinden (annihilieren). Falls nun gälte, so würden die zwei Teilchen eine Art gravitativen Dipol bilden. Die Dipole richteten sich in einem äusseren Gravitationsfeld aus, ähnlich wie sich in dielektrischen Materialien die Dipole nach dem äusseren elektrischen Feld ausrichten. Dabei gäbe es aber einen entscheidenden Unterschied: anders als in der Elektrizität würden sich im Falle der Anti-Gravitation gleiche Teilchen anziehen (sprich Teilchen und Teilchen, Antiteilchen und Antiteilchen) und ungleiche Teilchen abstossen (sprich Teilchen und Antiteilchen). Daraus würde folgen, dass die Polarisation des Vakuums das Gravitationsfeld weiter verstärken würde. Dies würde erklären, wieso die “zu schnell” um das Zentrum einer Galaxie rotierenden Himmelskörper auf ihren Bahnen gehalten werden: das Gravitationsfeld ist in den Armen der Galaxien grösser als wir ohne Berücksichtigung der Gravitationsdipole annehmen. Die anomalen Rotationsgeschwindigkeiten könnten also so erklärt werden, ohne “unsichtbare Masse” in Form von Dunkler Materie postulieren zu müssen.

Hajdukovics Erklärungsversuch steht und fallt natürlich mit der Verletzung des Äquivalenzprinzips für Antimaterie. Im Moment wird die Antiteilchen-Gravitation in mehreren Experimenten am CERN intensiv erforscht,  ein weiteres Experiment am PSI ist in Planung. Diese werden hoffentlich die möglichen Werte des Massenverhältnisses  wesentlich einschränken können, dabei vielleicht zudem unser Verständnis von Gravitation grundlegend ändern und die Postulation der Dunklen Materie in Frage stellen.

Als Abschluss dieses Beitrags möchte ich auf einen Cartoon von xkcd verweisen (xkcd.com):

Der Text dazu: “Of these four forces, there’s one we don’t really understand.” “Is it the weak force or the strong –” “It’s gravity.”

Quellen

• Touboul, P. et al.:  “MICROSCOPE Mission: First Results of a Space Test of the Equivalence Principle,” Physical Review Letters, vol. 119, iss. 23, id. 231101, 2017.
• Amole, C. et al. (ALPHA collaboration): “Description and first application of a new technique to measure the gravitational mass of antihydrogen,” Nature Commun, vol. 4, 2013.
• D.S. Hajdukovic: “Is dark matter an illusion created by the gravitational polarization of the quantum vacuum?,” Astrophysics and Space Science, vol. 334, no. 2, p. 215-218, 2011.
• Wikipedia: “Dunkle Materie.” Verfügbar unter https://de.wikipedia.org/wiki/Dunkle_Materie.

Quelle Beitragsbild: Master Isaac Newton in His Garden at Woolsthorpe, in the Autumn of 1665, Robert Hannah (1812–1909), artuk.org.